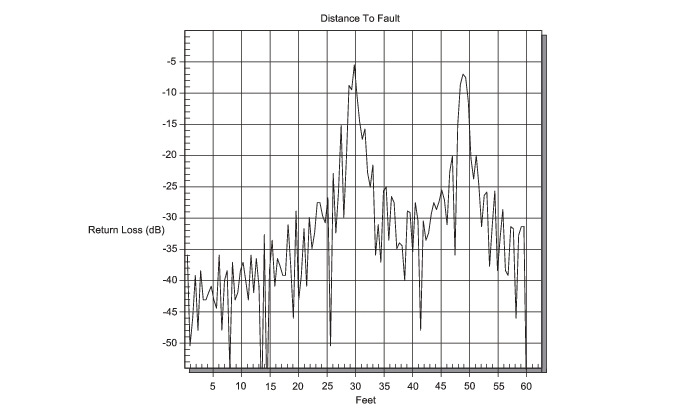
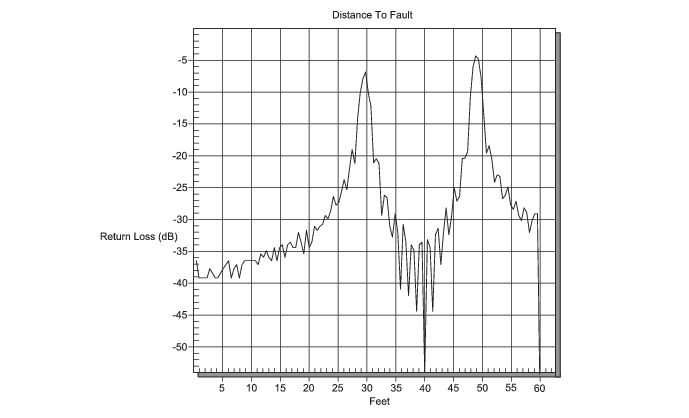
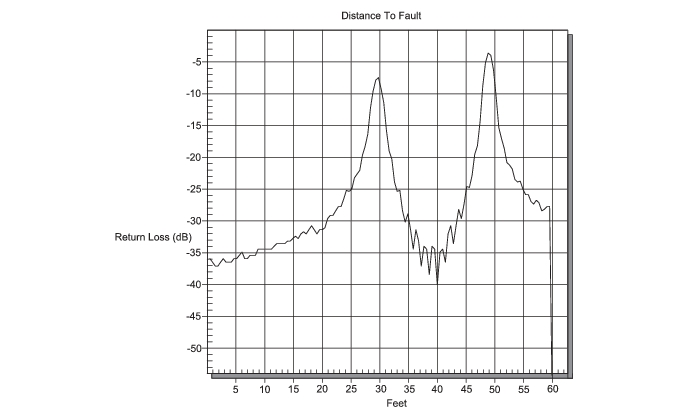
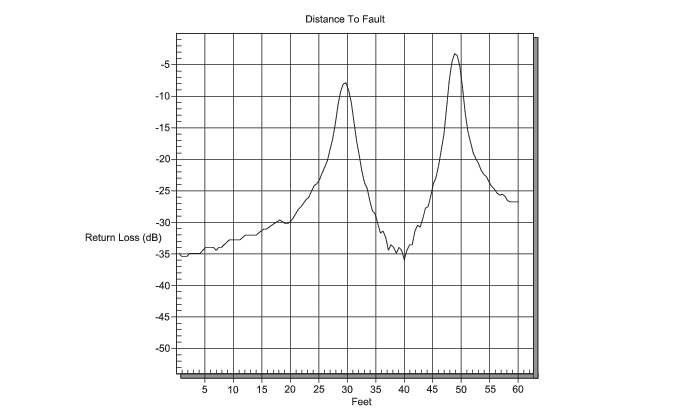
The theoretical requirement for inverse FFT is for the data to extend from zero frequency to infinity. Side lobes appear around a discontinuity due to the fact that the spectrum is cut off at a finite frequency. Windowing reduces the side lobes by smoothing out the sharp transitions at the beginning and at the end of the frequency sweep. As the side lobes are reduced the main lobe widens thereby reducing the resolution.
In situations where a small discontinuity may be close to a large one, side lobe reduction windowing should be used. When distance resolution is critical, windowing can be reduced.
